Derawi Biometrics

During the past years of increased use of biometric to authenticate or identify people, there has also been a similar increase in use of multimodal fusion to overcome the limitations of single-modal biometric system.  Multi-modal and Multi-biometric fusion is a way of combining two biometric modalities into one single wrapped biometric to make a unified authentication decision. Several of applications in the real world require a higher level of biometric performance than just one single biometric measure to improve security. These kinds of applications will replace and prevent national identity cards and security checks with fusion for example air travel, hospitals and et cetera. And for the individual who are not able to give a stable biometric to an application, then provision is needed.

The use of fused biometric measurement gives a substantially improved technical performance and reduced risk than uni-modal biometric sensors, algorithms or modalities. The book with Ross et al., Handbook of Multi- biometrics and the ISO document of  Multimodal and Other Multibiometric Fusion (ISO/IEC TR 24722:2007) , provide a good overview within this field and which will be summarized in the following.

There are several benefits when combining multiple biometric systems. The cohesive decision proposes a more significant improvement in precision and simultaneously reduces the FAR and FRR. The second benefit is that the more biometric attributes we apply the harder it is to spoof them, such that the impostor does not have any influence of the biometric used and at the same time makes the verification harder to grant. Third benefit is the reduction of noisy input data, such as a humid finger or a dipping eye-lid, since if one the input is highly noisy, then the other biometric might have a very high quality to make an overall reliable decision.  This can also be seen as the fault-tolerance, that is, to continue operating properly in the event of the failure if one system breaks down or compromised then the other might be sufficient to keep the authentication process running.

Levels of Combination

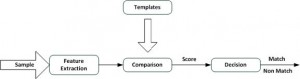
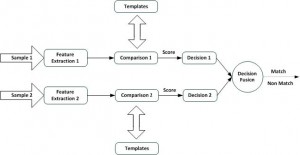
The ways in which biometric systems can be combined are numerous. But as a basis for the definition of levels of combination in multi-biometric systems, we first introduce the single-biometric process and its building blocks. Figure 1 shows the block diagram of a single-biometric process.

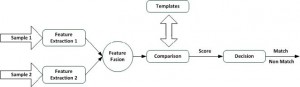
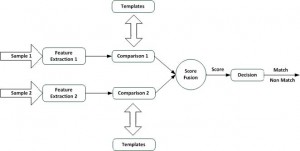
Usually a biometric system reads from the user an input sample, extracts features and compares them to a template to create a match score. This score explains how well the extracted features from the sample match a given template, and is compared to a threshold to determine if the authentication succeeded. So if the match is below the threshold then the authentication fails, otherwise it succeeds. These processing steps make it possible to unite multiple biometric at different level of abstraction. The layout for a multi-modal system is shown in Figure 2. The diagram shows the various levels of fusion for combining multiple biometric systems. The three fusion levels are:  fusion at the feature extraction level, fusion at the comparison score level and finally fusion at the decision level.

Generally the match score fusion approach is the method which is mostly used. The reason for that is that match scores are easy to access and there are many ways of combining them, from simple to complex implementations. In addition, match scores present rich information about the input. But match scores are not always to be obtained from all biometric systems. On the other hand they suffer from some commercial systems, which only provide the final authentication decision. Therefore it will be impossible to gain this kind of information.

To be capable to fuse two biometric data it is also necessary to know how to gain it. For that the term biometric data is used for any level of abstraction. The term biometric data is defined to be a feature vector, a match score or a decision. The next is how to obtain the biometric data from multiple sources and for that there are several methods:

Fusion in biometric has shown increased reliability, i.e. where fused system gives better results than single biometric systems. This has been shown by Hong et al. with system consisting of a face recognition system (identifying the top n users) which further is verified by a fingerprint scanner. They concluded that the fused system provided a lower FRR’s than the individual systems, for several different FAR values. For a FAR of 1%, the face recognition system had a FRR of 15.8% and the fingerprint scanner had a FRR of 3.9% while the fused system had a FRR of only 1.8%.

Advanced Decision-level Fusion

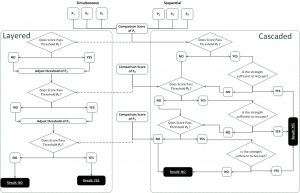
The simple decision-level fusion is based upon an accept/reject decisions for each sample. The two sub groups of advanced decision-level fusion are divided into the following systems:

• Layered System uses individual biometric scores to determine the pass/fail thresholds for other biometric data processing.
• Cascaded Systems uses pass/fail thresholds of modality-specific biometric samples to determine if additional biometric samples from other modalities are required to reach an overall system decision.

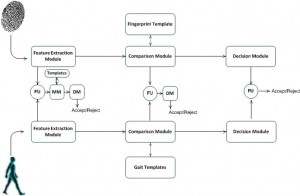
The two subgroups decision-level fusion are shown in Figure 6 and will be explained in further details in the following.

Independent of whether the presentation is simultaneous or sequential, the match score of P1 enters the layered system. The system processes the score against the system defined threshold:

Independent of simultaneous or sequential presentation, cascaded systems rely on at least one biometric sample. If the first sample does not meet the requirements, additional samples are matched. Match score P1 enters the system and is matched against the threshold for sample P1:

Score Normalization and Score Fusion Methods

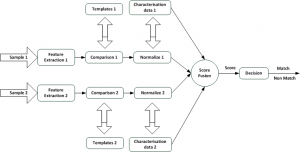
As mentioned earlier in this chapter, there are several types of fusion (decision level, score level or feature level). Academics and industry researchers have shown that fusion at the score level fusion is the most effective in delivering increased accuracy. The score fusion methods that will be shown in this section consist of two stages. In the initial stage, the output score of $S_i$ generated by an algorithm is mapped onto a new score $S_i^`$. This is usually referred to as the normalization step, but it is not normalization in the regular mathematical sense of the word. (This step is sometimes referred to as score mapping.) Score normalization usually requires that several factors are known before the normalization can be done. In the simplest case, the range of the scores generated by the algorithm needs to be known. For example, if algorithm X generates scores between 0 and 100, a typical normalization step would be to divide the original score by 100. More complex normalization schemes would require a priori knowledge about the raw score distributions.

In the second stage, is the fusion itself. Fusion usually takes as input one score per algorithm or modality and produces a single output score. There are many ways of fusing a set of scores to obtain a single score but in this project we will use the normalization and fusion algorithms according to ISO-standard ISO/IEC TR 24722.  The simpler fusion methods include the average, the minimum, the maximum, and so on. More complex score fusion algorithms could require all inputs to be from a well defined distribution type, or could even require the raw score distributions as input which can be seen in Appendix \ref{app:normalization_fusion} \ref{table:fusion_methods}

Score Normalization

Score normalization is used to map the scores of each simple-biometric into one common domain.  Some of the methods are based on the Neyman-Pearson lemma, with simplifying assumptions. Mapping scores to likelihood ratios, for example, allows them to be combined by multiplying under an independence assumption. The other approaches may be based on modifying other statistical measures of the match score distribution.

The normalization parameters used can be determined using a “fixed training set” or “adaptively based feature vector”. What is relevant to know is that score normalization is related very close to score-level fusion since it affects how scores are combined and interpreted in terms of biometric performance. As in \cite{fuse1}:

• The comparison scores at the output of the individual matchers may not be homogeneous. For example, one matcher may output a distance (dissimilarity) measure while another may output a proximity (similarity) measure.
• Further, the outputs of the individual matchers need not be on the same numerical scale (range);
• Finally, the comparison scores at the output of the matchers may follow different statistical distributions.

Figure 7 illustrates a score-level fusion framework for processing two biometric samples, taking normalization into account.

Table 1 and 2  shows a part of many normalization methods that can be seen in Appendix \ref{app:normalization_fusion} Table \ref{table:app_normalization}.

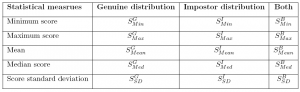
• Min-Max Normalization: Min-max normalization is used simply to transform scores into the same numerical range. In this case, scores should usually be between 0 and 1. The data elements used in this case is the maximal value $S_{Max}^B$ and minimal value $S_{Min}^B$ from the working dataset.
• Z-Score Normalization: When the score distributions for the genuine and impostor tests are approximately Gaussian distributions, one can use Z-Score mapping to shift the distribution such that the impostor distributions fall almost on top of each other.  The data elements in this normalization are the mean $S_{Mean}^I$ of the Gaussian and the standard deviation $S_{SD}^I$. The normalization assumes normal distribution and is symmetric about mean.
• Median Absolute Deviation Normalization: Instead of using the average and standard deviation of the score distributions, one can also use the median and MAD (median absolute deviation), respectively, as parameters for the Z-score normalization. This method is more robust against outliers, but is only of use if the distributions are close to Gaussian. Otherwise it is impossible to map different algorithm scores onto similar distributions. The data element in this normalization is the median $S_{Med}^B$.  The median $S_{Med}^B$ of a score distribution is the middle value in the list of sorted scores.
• Hyperbolic Tangent Normalization: Is a basic algorithm of the Z-score but referred with a tanh-estimator and where the $S_{Mean}^G$ and  $S_{SD}^G$ are the mean and standard deviation of a weighted genuine score distribution.

Score Fusion

When individual biometric matchers output a set of possible matches along with the quality of each match (match score), integration can be done at the match score level. This is also known as fusion at the measurement level or confidence level. The match score output by a matcher contains the richest information about the input biometric sample in the absence of feature-level or sensor-level information. Furthermore, it is relatively easy to access and combine the scores generated by several different matchers. Consequently, integration of information at the match score level is the most common approach in multi-modal biometric systems. Table \ref{table:app_fusion} in Appendix \ref{app:normalization_fusion} provides an outline of several score fusion methods and their associated needs for data that characterize the matcher performance. Table 3 is an outline from the appendix which will be used in this project.